Вопрос можно поставить и так: зачем изучать математику школьникам, если они выбрали профессию, в которой не будет места вычислениям, анализу чисел и фигур – всему тому, с чем в обиходном сознании связывают математику?
Кстати, представление о математике, как о науке, посвященной только числам и фигурам, неточное и неполное: в действительности математика изучает структуры и отношения неких объектов, получаемых идеализацией реальных, а зачастую и не только реальных предметов.
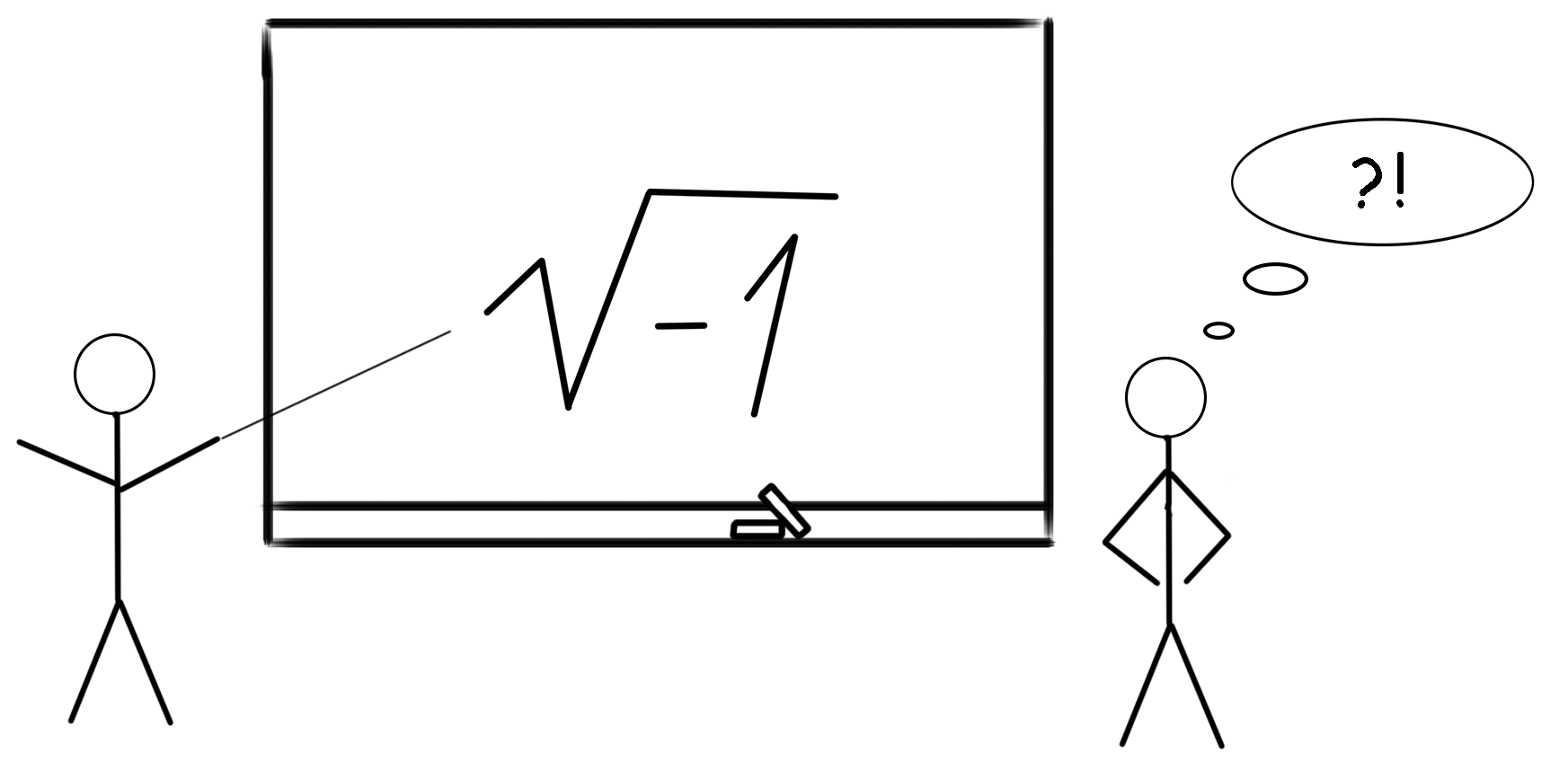
Взять хотя бы квадратный корень из минус единицы. В обиходной жизни не встретить число, которое при умножении само на себя дало бы отрицательный результат. Раз так, то этот самый корень из минус единицы – не более чем выдумка. Недаром его называют мнимой единицей. На первый взгляд, практической пользы от таких фантазий быть не может, но на самом деле мнимые числа и объединение их с действительными числами (комплексные числа) стали основой методов, которые честно трудятся в электротехнике, в механике сплошных сред (за ней стоят, машиностроение, авиация). А ведь сначала казалось: «выдумка». Так что, не стоит спешить с выводами.
Вернемся к поставленному вопросу. Зачем заниматься математикой гуманитариям, медикам, биологам, художникам, музыкантам? Зачем мучать математикой будущую преподавательницу иностранного языка или врача? Часто, когда будущих не математиков пытаются убедить в пользе изучения математики, им предлагают простенькие аргументы: а как же, например, дипломат, не зная математики, подсчитает сдачу в булочной или решит, сколько колючей проволоки закупить для ограды садового участка? Не убедительно! Сдача в булочной в наши дни подсчитывается автоматически (при оплате банковской картой в ней и вовсе нет нужды), колючая проволока вышла из моды, а сам пример с ограждением участка навеян рассказом о том, как геометрия родилась из потребностей землемеров много веков тому назад где-то в очень древнем мире. Разумеется, все мы очень рады за живших когда-то греков и египтян, но уж очень давно и далеко от нас это было… Неактуально!
Действительно, дело не в сдаче, не в проволоке и не в землеустройстве! В первую очередь, математика в школе полезна тем, что она действенно и наглядно учит тому, как можно создать стройную систему знаний на основе всего лишь нескольких положений, принимаемых без доказательства (на веру, или в силу очевидности). Положения эти называются аксиомами. Все новые знания в математике (например, в курсе геометрии) получают из аксиом исключительно рассуждениями, используя такой инструмент, как логика. Разбирая доказательство очередной теоремы, мы осваиваем навык логического мышления, позволяющий рассуждать последовательно, думать непротиворечиво и добывать в процессе рассуждений новые знания. Это гораздо важнее, чем сама теорема, а приобретаемый при этом навык рассуждения может сильно повлиять на личность школьника. Если он (школьник) действительно освоил курс математики, а не подменил его бесполезной зубрежкой определений и формул, то для него всегда будет ощутимо различие между фактом, добытым рациональными рассуждениями, и фактом, полученным в виде стороннего мнения.
Математика, конечно же, полезна своими практическими приложениями, но главный приз за ее освоение в школе – именно овладение навыками логического мышления. Это важнее, чем, например, возможность подсчитать площадь треугольника по трем его сторонам. Здесь – наш поклон достопочтенному Герону и формуле его имени, которую он вывел в Александрии еще в I веке нашей эры (правда, говорят, что эта формула была известна и ранее), но дело не столько в самой формуле Герона, сколько в том, что, выводя ее, школьник учится мыслить. Это умение – одна из главных привилегий человека разумного. Без него и дипломат, и биолог, и врач, и лингвист будут представлять собой грустное зрелище. Отсутствие навыка логического мышления делает из человека инвалида, и эта инвалидность не менее тяжелая, чем та, что вызвана физическими проблемами.
Разумеется, владение логикой, это еще далеко не все, что формирует личность, но без нее плохо. Можно долго спорить, кто лучше: человек толковый, но плохой, или человек бестолковый, но хороший; нужно стремиться, чтобы из ребенка вырос человек толковый и хороший, и изучение математики поможет в достижении этой цели.
Математика не всем дается сразу и легко. Бывает, что дети (часто под давлением старших) пытаются свое неумение рассуждать логически компенсировать усердием, желанием все не столько понять, сколько зазубрить. От этого бывает только хуже: обилие заученных, не охваченных пониманием фактов, дат, терминов и определений превратится в тяжелый и бесполезный груз. Наверняка вам встречались, например, юристы, выбравшие свою профессию «от обратного» (только потому, что «не давалась математика»). Получив диплом, они не могут логически осмыслить хитросплетения законов и в своей профессиональной деятельности опускаются до уровня письмоводителя…
Умение логически мыслить – важный, но не единственный результат добросовестных занятий математикой в детстве. Есть и другие ценные награды, за которые стоит побороться. Если вы, читатель, уже взрослый человек, то вспомните, как не всегда легко вам давались азы алгебры: формулы сокращенных преобразований (квадрат суммы, разность квадратов) в сочетании с правилами раскрытия скобок, приведения подобных членов. Сколько досадных ошибок пришлось вам сделать не оттого, что было непонятно, а лишь потому, что просто не доставало воли, внимания и организованности, чтобы не забыть все подобные члены при суммировании. Школьный курс математики поможет повысить степень организованности, научит сосредотачиваться над задачей – это пригодится везде и всем.
Математика не только учит собранности, самодисциплине и логике. Она открывает возможности изучения многих дисциплин. Те идеализированные объекты, которые она изучает, зачастую оказываются моделями самых различных, очень не похожих друг на друга предметов и явлений.
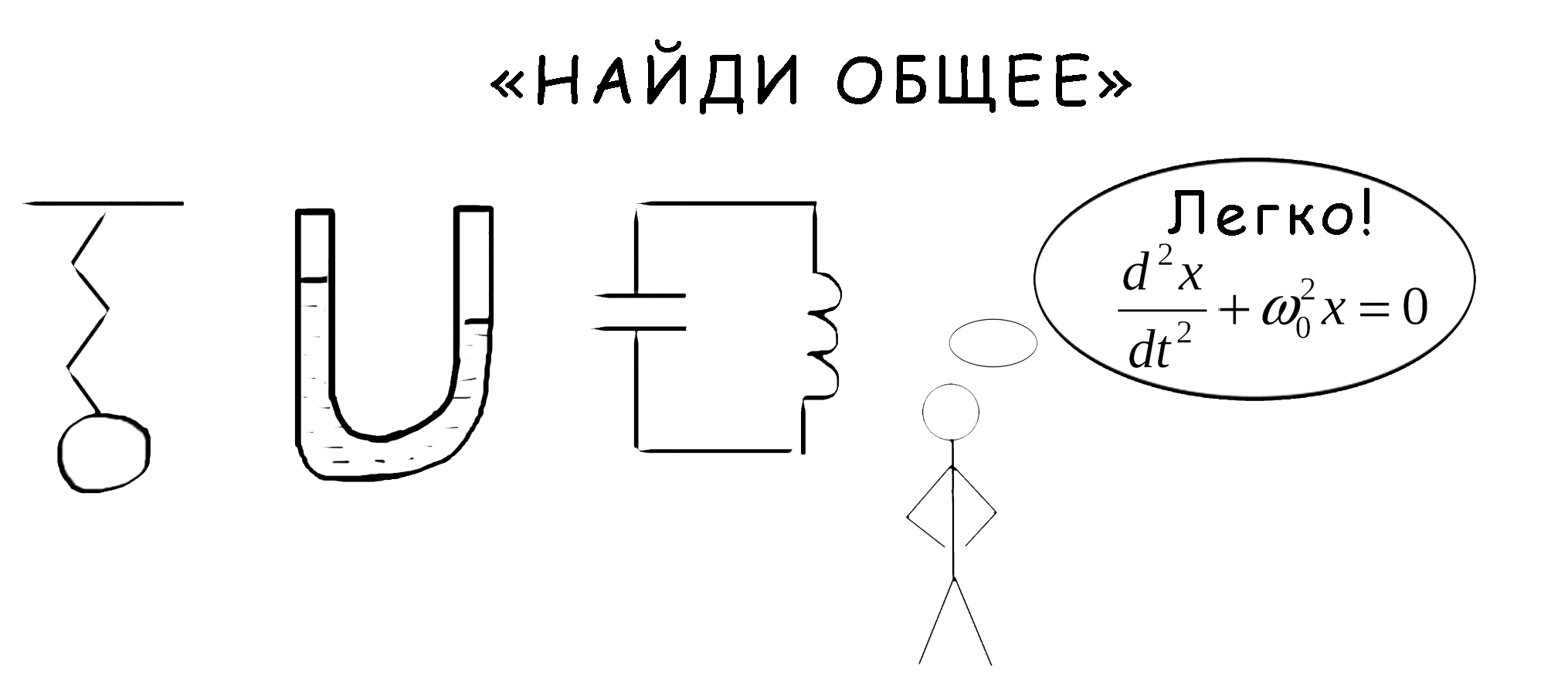
Вот лишь самый простой пример. Грузик, подвешенный на пружинке, будет совершать колебательные движения, если растянуть пружинку и отклонить грузик от положения равновесия, а потом предоставить его самому себе. Анализ движения этого грузика приводит к дифференциальному уравнению второго порядка (это уравнение связывает величину отклонения грузика от положения равновесия с ее второй производной по времени – ускорением). Оказывается, точно таким же уравнением описывается движение маятника. Но и это не все! Колебания уровня жидкости, частично заполняющей U-образную трубку, расположенную в вертикальной плоскости, описываются все тем же дифференциальным уравнением второго порядка (хоть эта трубка с жидкостью вовсе не похожа ни на грузик, ни на маятник). Продолжаем далее. Если заряженный конденсатор замкнуть на концы провода, намотанного на сердечник, то по образовавшемуся контуру начнет разгуливать ток, сила которого также описывается тем же самым дифференциальным уравнением второго порядка (сила тока, как и величина отклонения грузика от положения равновесия, будет изменяться по колебательному закону).
Отсюда важный вывод. Изучая математику, мы осваиваем инструментарий для изучения многих других наук, исследующих материальный (и не только материальный) мир. В первую очередь это физика, которая, можно сказать, полностью математизировалась. В полной мере это относится и к тем наукам, которые раньше воспринимались, как разделы физики, но впоследствии развивались настолько самостоятельно, что стали отдельными научными дисциплинами: механика твердого тела, гидро- и аэродинамика.
В последние десятилетия математические методы проникли в такие науки, где математику, можно сказать, «не ждали». Всего лишь век тому назад экономика была совсем в стороне от математики (ну, разве что, экономисты признавали важность арифметики для получения статистических данных), но сейчас серьезные экономические исследования очень часто включают в себя разработку и использование математических моделей, анализ которых обладает предсказательной силой. Примерно то же происходит в общественных науках. Интересный пример из этой области: появились математические исследования, в которых с помощью методов теории вероятностей проанализированы неизбежные в любом голосовании отклонения от средних результатов. Эти исследования позволили выявить регионы с так называемым «аномальным» голосованием, где разброс результатов голосования отличается от того, что наблюдается в среднем по стране. Удивительным образом список регионов с таким аномальным голосованием совпал со списком так называемых «электоральных султанатов», из которых поступает максимальное количество сигналов о давлении администрации на избирателей и на вбросы в процессе голосования.
Современные исследования в области физиологии (в том числе и применительно к человеку) все чаще опираются на математические модели. С их помощью добываются результаты, помогающие понять закономерности функционирования живых систем. Эти относительно новые направления уже применяются в медицине: разработаны методы математической поддержки процесса постановки диагноза, а также методы предсказания развития опасных осложнений после инфаркта миокарда, методы построения неотложной оперативной тактики при кровотечениях, вызванных язвой желудка. А вот совсем другой пример, но также из области медицины. Математические методы теории тонкостенных оболочек помогли при разработке методов коррекции зрения с помощью лазерной микрохирургии.
Эта статья адресована не только нынешним школьникам, но и их родителям. Если у вашего ребенка возникли проблемы с освоением математики в школе, не нужно торопиться с вердиктом «У него нет математических способностей, наверно, он гуманитарий». И уж вовсе неправильно уговаривать в этом «героя событий» и вместе с ним принимать порочный метод «отбытия номера» вместо освоения математики. Совершив эту ошибку, вы заложите предпосылки того, что ваш ребенок много чего не доберет как личность, а это будет очень плохо и досадно даже в случае, если он выберет совсем нематематическую профессию.
Вполне возможно, что возникшие у школьника проблемы с математикой являются следствием тех комплексов, которыми школьник обрастает, потерпев ряд неудач из-за банальной невнимательности. Если так, то курс занятий с хорошим репетитором может не только быстро выправить ситуацию с успеваемостью, но и помочь ребенку почувствовать уверенность в своих силах, ощутить интерес к этой самой логичной из всех наук.




Комментарии:
Комментировать